BrainVoyager v23.0

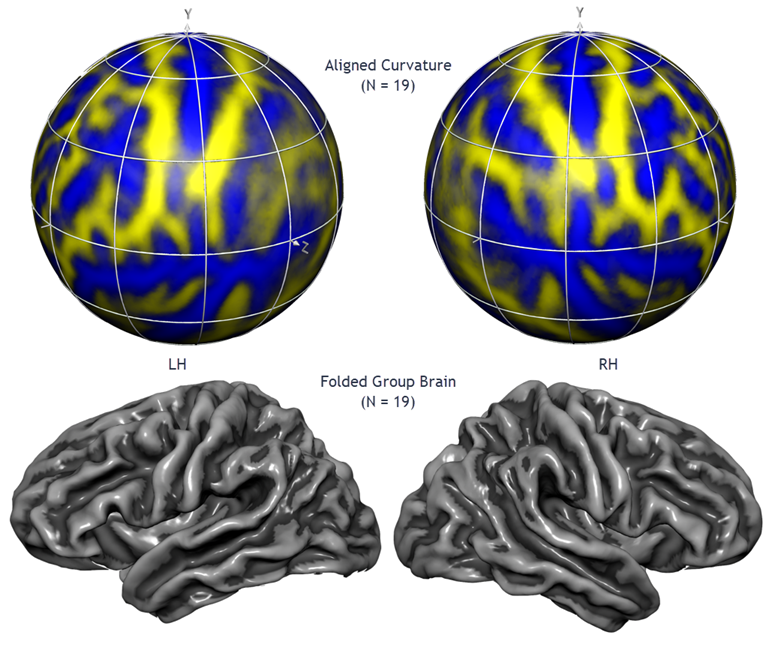
Cortex-Based Alignment of Sulci and Gyri

Introduction

A good match between corresponding brain regions is important for many applications including group-level statistical data analysis. Group analysis in Talairach or MNI space suffers, however, from a coarse alignment between subjects' brains producing suboptimal, and sometimes even misleading group maps due to extensive spatial smoothing. While functional areas are not precisely predictable from macroanatomical landmarks, it has been shown for areas V1 and motor cortex (Fischl et al., 1999) and for many other areas (Frost & Goebel, 2012) that a cortical matching approach substantially improves statistical group results by reducing anatomical variability. BrainVoyager offers an advanced, high-resolution, approach to align brains using macro-anatomical (curvature) and optionally functional information of the cortex (Goebel et al., 2002, 2004, 2006; Frost & Goebel, 2012, 2013). Since the curvature of the cortex reflects the gyral/sulcal folding pattern of the brain, this brain matching approach essentially aligns gyri and sulci across brains when initialized with an approximate (e.g. MNI or Talairach-based) pre-alignment step. The figure above, for example, shows the average brain (folded cortex) of a group of 19 left and right hemipspheres after curvature-driven cortex-based alignment (Rosenke et al., 2021).

Background

Curvature-driven cortex-based alignment (CBA) operates in several stages. The reconstructed folded cortical representations of each subject and hemisphere constitute the input of the alignment procedure. In the first step, these folded representations are morphed into a spherical representation, which provides a parameterizable surface well-suited for across-subject non-rigid alignment. Each vertex on the sphere (spherical coordinate system) corresponds to a vertex of the folded cortex (Cartesian coordinate system) and vice versa. The curvature information computed in the folded representation is preserved as a curvature map on the spherical representation. The curvature information (macroanatomical folding pattern) is produced in several fine-to-coarse versions with minimal and more extensive smoothing along the surface in order to provide spatially extended gradient information driving intercortex alignment. Alignment proceeds by moving vertices to minimize the mean squared differences between the curvature of a source and a target sphere at corresponding locations. The essential step of the alignment is an iterative procedure following a coarse-to-fine matching strategy. Alignment starts with highly smoothed curvature maps and progresses to only slightly smoothed representations. Starting with a coarse alignment of curvature maps on the sphere as provided by volumetrically normalized brains in MNI or Talairach space and an optional rigid spherical alignment step, it is ensured that at the begin the smoothed (coarse) curvature maps of source and target spheres possess enough curvature overlap for a locally operating gradient-descent procedure to converge without user intervention (Goebel et al., 2002, 2004, 2006; Frost & Goebel, 2012). Visual inspection and a measure of the averaged mean squared curvature difference reveal that the alignment of major gyri and sulci can be achieved reliably by this method. Smaller structures, visible in the curvature maps with minimal smoothing, may not be completely aligned since they often reflect idiosyncratic differences between the subject's brains, such as continuous versus broken sulci.

Note that the alignment requires the specification of a target brain to which source brains are aligned. The program offers two approaches to define the target brain. In the explicit target approach, one sphere is selected as a target to which all other spheres are subsequently aligned. The target sphere can be derived from one of the brains of the investigated group or from a special reference brain. Although tests have shown that alignment results are very similar when using curvature maps from different individual target spheres, the selection of a specific target brain might lead to results that are dependent partially on the chosen target brain, especially in case that the selected brain contains many regions with a non-typical folding pattern. One solution consists in using an averaged (curvature) atlas brain (one mesh per hemisphere) as the target (fs-average or bv-average, see Rosenke et al. 2021), which has been itself created via cortex-based alignment from a large number of individual brains.

As another option, the moving target group averaging approach does not require the selection of an individual (or atlas) target sphere since the goal function is specified as a moving target computed repeatedly during alignment as the average curvature across all hemispheres at a given alignment stage. The procedure starts with the most coarse curvature maps. Then the next finer curvature maps are used and averaged with the obtained alignment result of the previous level. This iterative coarse-to-fine refinement procedure results in a new group averaged curvature map and a folded brain that represents the group to which all individual brains are cortically aligned.

In analogy to volumetric alignment, the established anatomical correspondence mapping between vertices of the cortices can be subsequently used to align functional data of subjects represented in mesh time course (MTC) files. The cortically aligned mesh time course data can be statistically processed with the same fixed and random-effects GLM calculation tools that are used for the analysis of volume time course datasets. Furthermore, surface maps (SMPs) and Patches-Of-Interest (POIs) defined on cortex meshes of individual subjects can be transformed into group-aligned cortex space.

Application

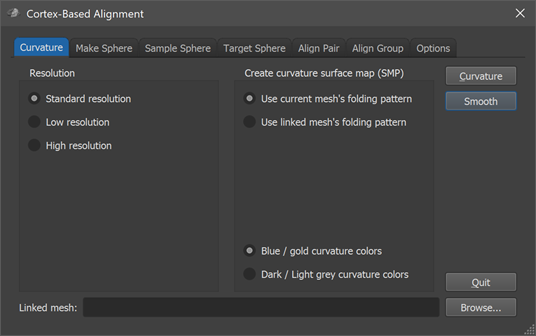
Curvature-driven CBA is performed using the Cortex-Based Alignment dialog (see screenshot above) that contains several tabs for the various stages of this process. The dialog can be opened via the Cortex-Based Alignment item in the Meshes menu. To use the curvature-driven cortex-based approach for inter-subject alignment, follow these steps:

After these essential steps, you can perform further procedures to quantify and visualize the achieved alignment. You can also proceed with cortex-based statistical data analyses using the created alignment files with created mesh time course (MTC) files.

In case that information about corresponding regions is available from independent functional localizer runs, it is possible to integrate that information. For more details, see topic Functionally Informed Cortex-Based Alignment.

Resolution of Aligned Space

The curvature-driven inter-subject alignment is performed using generic spherical meshes that are used to sample the original subject-specific (morphed to sphere) meshes in a common space. The options in the Resolution field in the first (Curvature) tab of the Cortex-Based Alignment dialog allow to select one of 4 resolution levels determining the number of vertices used for generated spherical representations. In most cases, the Standard resolution option (default) should be used that will create sphere meshes with 40962 vertices and 81920 trianges. In case that one works with high-resolution (sub-millimeter) anatomical data, one might consider using the High resolution option that will create sphere meshes with 163842 vertices and 327680 triangles, or even the Ultra-high resolution option with 655362 vertices and 1310720 triangles. The Low resolution option is recommended in case one wants to perform EEG / MEG source imaging in multi-subject aligned cortex space (10242 vertices, 20480 triangles).

A non-standard resolution should be chosen at the begin of cortical alignment, i.e. when inflating folded meshes to spheres that are sampled by a generated standard sphere. One should also check that the desired resolution is selected in the Cortex-Based Alignment dialog in case one re-enters the dialog to avoid incompatible sphere resolution for different hemispheres. The chosen setting not only influences the resolution of the generated shpere meshes but also sets parameters to optimize speed and robustness for the non-linear alignment process.

References

Fischl B, Sereno, M.I., Tootel, R.B.H., and Dale, A.M. (1999). High-resolution intersubject averaging and a coordinate system for the cortical surface. Human Brain Mapping, 8, 272-284.

Frost, M. & Goebel, R. (2012). Measuring structural-functional correspondence: Spatial variability of specialised brain regions after macro-anatomical alignment. NeuroImage, 59, 1369-1381.

Goebel, R., Staedtler, E., Munk, M.H.J., Muckli, L. (2002). Cortex-based alignment using functional and structural constraints. NeuroImage Supplement.

Goebel, R., Hasson, U., Harel, M., Levy, I., Malach, R. (2004). Statistical analyses across aligned cortical hemispheres reveal high-resolution population maps of human visual cortex. NeuroImage Supplement (Human Brain Mapping, Budapest).

Goebel, R., Esposito, F. & Formisano, E. (2006). Analysis of functional image analysis contest (FIAC) data with Brainvoyager QX: From single-subject to cortically aligned group general linear model analysis and self-organizing group independent component analysis. Human Brain Mapping, 27, 392-401.

Rosenke, M., van Hoof, R., van den Hurk, J., Grill-Spector, K., Goebel, R. (2021). A Probabilistic Functional Atlas of Human Occipito-Temporal Visual Cortex. Cerebral Cortex, 31, 603–619.