BrainVoyager v23.0

High-Pass Filtering of Design Matrix

High-pass filtering is one of the most important preprocessing steps as described in topic Temporal High-Pass Filtering in the Preprocessing chapter and in topic Adding High-Pass Filter Confound Predictors. It is, however, important that the high-pass filter does not remove task-related effects. While knowledge of the stimulation protocol might be enough to specify the right high-pass filter, a direct test whether a certain design matrix is affected by a specific high-pass filter would be a useful tool. This can be performed in BrainVoyager QX by applying a high-pass filter to the design matrix. If the design matrix looks the same before and after application of the high-pass filter, it is save to assume that task-related effects are not "touched" by the high-pass filter. If an effect of the filter is observed, the cut-off frequency of the high-pass filter should be reduced. Sometimes it might be tolerable to accept a mild affect of the high-pass filter on the design matrix; in this case it is important to use the filtered design matrix (and not the original one) for a GLM analysis in order to proceed in a statistically sound way.

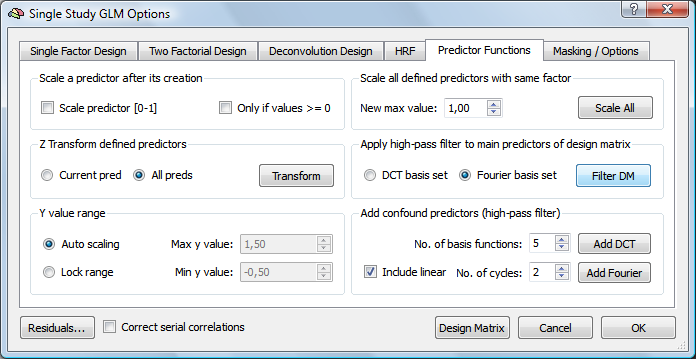
To test the effect of a specific high-pass filter, define or load a design matrix. If you plan to add confound predictors, defer this until the high-pass filter test has been made. To apply a filter, you may chose from one of two options available in the Apply high-pass filter to main predictors of design matrix field of the Predictor Functions tab of the Single Study GLM Options dialog (see snapshot above); if you select the Fourier basis set option (default), a Fourier basis set is used to filter the design matrix; if you select the DCT basis set option, a discrete cosine transform (DCT) basis set is used for high-pass filtering. The number of cycles or number of basis functions must be specified using the No. of cycles or No. of basis functions spin box in the Add confound predictors (high-pass filter) field, respectively. Make sure to match the selected filter version and parameter according to the settings made during preprocessing. If you prefer performing the high-pass filter as part of statistical analysis, specify the filter in the same way as you intend to add (after the test) to the design matrix.

The snaphsot below shows one main predictor of the design matrix used to analyze the "Objects" sample data set obtained after clicking the Define Preds button in the Single Study General Linear Model dialog.

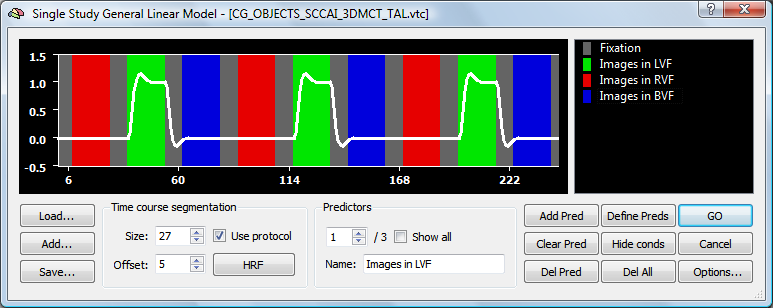
The following series of snapshots shows the effect of different high-pass filter settings on the selected predictor using the Fourier basis set option.

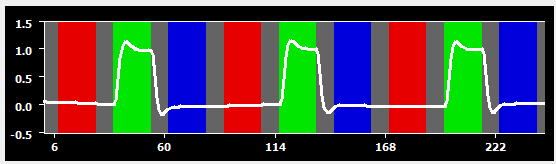
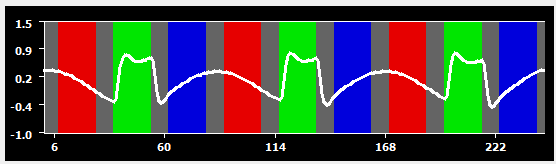
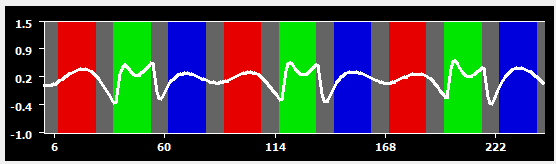
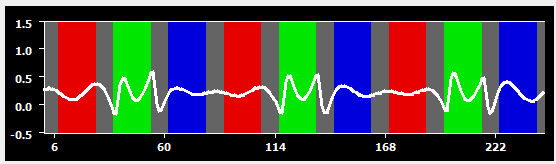
For the first plot, two cycles were used, which has almost no effect on the design matrix. This filter setting would, thus, be appropriate for the current study. When a Fourier filter with three cycles is used instead, a substantial effect of the filter is already noticeable (second plot); this happens because each condition is presented 3 times; since a block is, however, much shorter than the duration of one "up and down"of the three cycles frequency, the filter is not "able" to fully remove the block response, which requires higher frequencies. When a Fourier filter with six cycles is used (third plot), the filter largely removes the difference between the three conditions and the plateau of the modeled "green" predictor is only minimally different from the plateaus of the other two conditions. When a Fourier filter with nine cycles is used (fourth plot), almost all modeled signal fluctuations are gone and only the high-frequency sections at the begin and end of modeled block responses are still visible. This example shows that to be on the save side, the removed filter frequency should be lower than the minimum frequency of occurrence of a condition.