BrainVoyager v23.0

Probabilistic Maps and Maximum Probability Maps

Introduction

When performing fMRI group studies, it is useful to investigate the spatial consistency of activity patterns or regions-of-interest across subjects. One useful approach to quantify consistency is offered by the calculation of probabilistic (functional) maps. At each spatial location, such maps represent the relative number of subjects leading to significant task activity or exhibit the same region-of-interest. In a study of 20 subjects, for example, a value of 60% in a probabilistic functional map would indicate that 12 subjects activated the respective brain region. It is evident that the calculation of probabilistic functional (or other) maps depends to some extent on the chosen brain normalization method since probabilities are determined by counting how many subjects activate at the "same" spatial location. For volumetric normalization schemes, spatial coordinates (e.g. in Talairach or MNI space) address corresponding regions in the brains of different subjects. For cortex-based normalization schemes, aligned surface points (mesh vertices) are used to address corresponding brain regions. Relative to a good macro-anatomical alignment, probabilistic functional maps may reveal the spatial consistency of areas across subjects.

Probabilistic Functional Maps

In BrainVoyager, probabilistic maps can be calculated using volumetric maps (VMPs) or surface maps (SMPs) to quantify how many subjects surpass a statistical threshold at corresponding locations. For each subject, the same type of information must be represented in the provided maps per subject; in the context of a GLM analysis, for example, the same contrast(s) must be calculated for each subject, which can be easily performed as described in topic Creating Multi-Subject T and Beta Maps from Mult-Subject GLMs. Since volume or surface maps can also be created using several other tools (e.g. Independent Component Analysis, Granger Causality Analysis, Cortical Thickness Analysis), probabilistic maps provide a general means to evaluate the spatial consistency of effects across subjects. When subjects have been co-registered using cortex-based alignment, the surface maps of participating subjects must be transformed in group-aligned space prior to calculation of probabilistic maps. This step is not necessary when calculating GLM-based probabilistic surface maps since the cortex-based GLM performs the cortex-based alignment step implicitly, but it is necessary, e.g., for cortical thickness maps.

Probabilistic Maps of Regions-Of-Interest

Probabilistic maps can also be calculated based on regions-of-interests (ROIs) specified for each subject in volume (VOIs) or surface (POIs) space. When ROIs have been specified on subject's cortex (SPH) meshes, the POIs must be transformed first into group-aligned space prior to calculation of probabilistic maps. If corresponding VOIs or POIs have been defined for each subject, resulting probabilistic maps are likely more focal and easier interpretable than probabilistic maps from volume or surface maps. On the other hand, whole-brain (whole-hemisphere for cortex meshes) probabilistic maps calculated on the basis of subject's (statistical) maps may help to reveal consistent regions or extended networks across subjects at unexpected locations.

Visualizing Probabilistic Maps

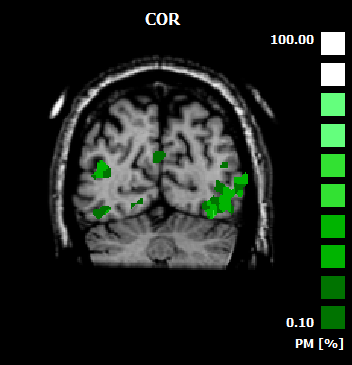
In order to properly represent probabilistic maps, the map type "PM" has been defined, which represents at each voxel or vertex a percent value in the range from 0 - 100. This map type is recognizable by the "PM" label in the displayed color bar as shown in the snapshot below. The threshold value can be changed as usual; if one wants, for example, to see only the locations in a probabilistic map where 50 or more percent of the subjects overlap, the Min threshold must be set accordingly in the Volume Maps or Surface Maps dialog. It is also possible to use the Increase Threshold and Decrease Threshold icons to modify the percent threshold. The information how many subjects were included in calculating a probabilistic map is provided in the DF 1 field of the Volume Maps and Surface Maps dialog (the degrees-of-freedom value is not used for any statistical calculation in case of a PM map). In order to see better transition zones in probabilistic maps, special look-up tables may be used; examples for a useful look-up-tables are provided in the "MapLUTs" folder (e.g. "ProbMap_Red.olt", "ProbMap_Green.olt", "ProbMap_Blue.olt"); each volume or surface map may have its own look-up-table (it is also possible to assign an individual color gradient for each map, which is interpolated between a specified "min" and "max" color).

Maximum Probability Maps and Creation of Atlases

Since version 20.6 of BrainVoyager maximum probability maps (MPMs) are calculated automatically when calculating probability maps for multiple ROIs (if not turned off). MPMs assign a single area label to a voxel or vertex corresponding to the ROI probability map with the hightest (maximum) probability value. In case that two or more probability maps have the same probability value at a voxel or vertex, a decision need to be made to which map the voxel or vertex belongs. To break such tie situations, the program inspects an increasing voxel/vertex neighborhood counting how often the respective ROIs are represented. While ties are less likely for statistical maps, they may occur frequently in case of VOI/POI based probability maps since only as many non-zero values can be calculated per voxel/vertex as subjects are available (prob_i = n_i/N_i*100 with n indicating the number of overlapping subjects for a specific map i and N the number of all included subjects). Breaking ties by inspecting voxel or vertex neighborhoods extents the functionality provided by the "winner" map function available in the Combine Maps dialog available for volume and surface space. The calculation of MPMs is especially useful to define boundaries between multiple overlapping probability maps (see example for VOIs and POIs in topics below). Since computed MPMs integrate all multi-subject source probability maps in one visualization of non-overlapping regions, they form the basis for building and visualizing custom brain atlases.

The following sections describe in more detail how to calculate: